Kolmogorov-Smirnov Test

A two-sample test using the Kolmogorov-Smirnov test statistic (ks_stat).

Usage

ks_test(a, b, nboots = 2000, p = default.p, keep.boots = T, keep.samples = F)

ks_stat(a, b, power = def_power)

Arguments

a

a vector of numbers (or factors -- see details)

b

a vector of numbers

nboots

Number of bootstrap iterations

p

power to raise test stat to

keep.boots

Should the bootstrap values be saved in the output?

keep.samples

Should the samples be saved in the output?

power

power to raise test stat to

Value

Output is a length 2 Vector with test stat and p-value in that order. That vector has 3 attributes -- the sample sizes of each sample, and the number of bootstraps performed for the pvalue.

Details

The KS test compares two ECDFs by looking at the maximum difference between them. Formally -- if E is the ECDF of sample 1 and F is the ECDF of sample 2, then $$KS = max |E(x)-F(x)|^p$$ for values of x in the joint sample. The test p-value is calculated by randomly resampling two samples of the same size using the combined sample.

In the example plot below, the KS statistic is the height of the vertical black line.

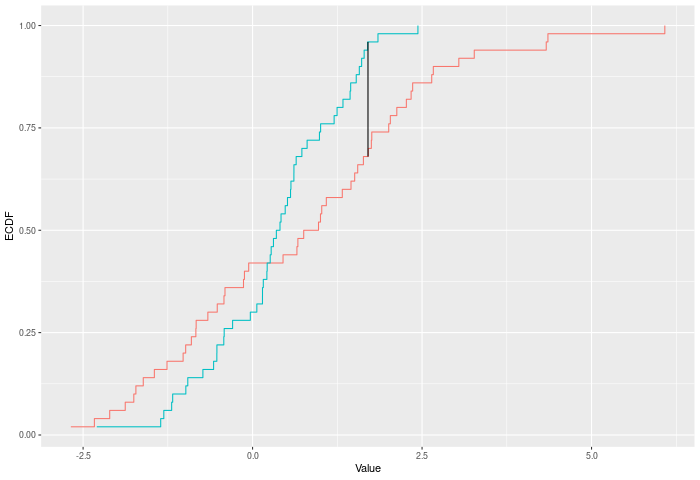
Inputs a and b can also be vectors of ordered (or unordered) factors, so long as both have the same levels and orderings. When possible, ordering factors will substantially increase power.

Functions

• ks_test(): Permutation based two sample Kolmogorov-Smirnov test

• ks_stat(): Permutation based two sample Kolmogorov-Smirnov test

See also

dts_test() for a more powerful test statistic. See kuiper_test() or cvm_test() for the natural successors to this test statistic.

Examples

set.seed(314159)
vec1 = rnorm(20)
vec2 = rnorm(20,0.5)
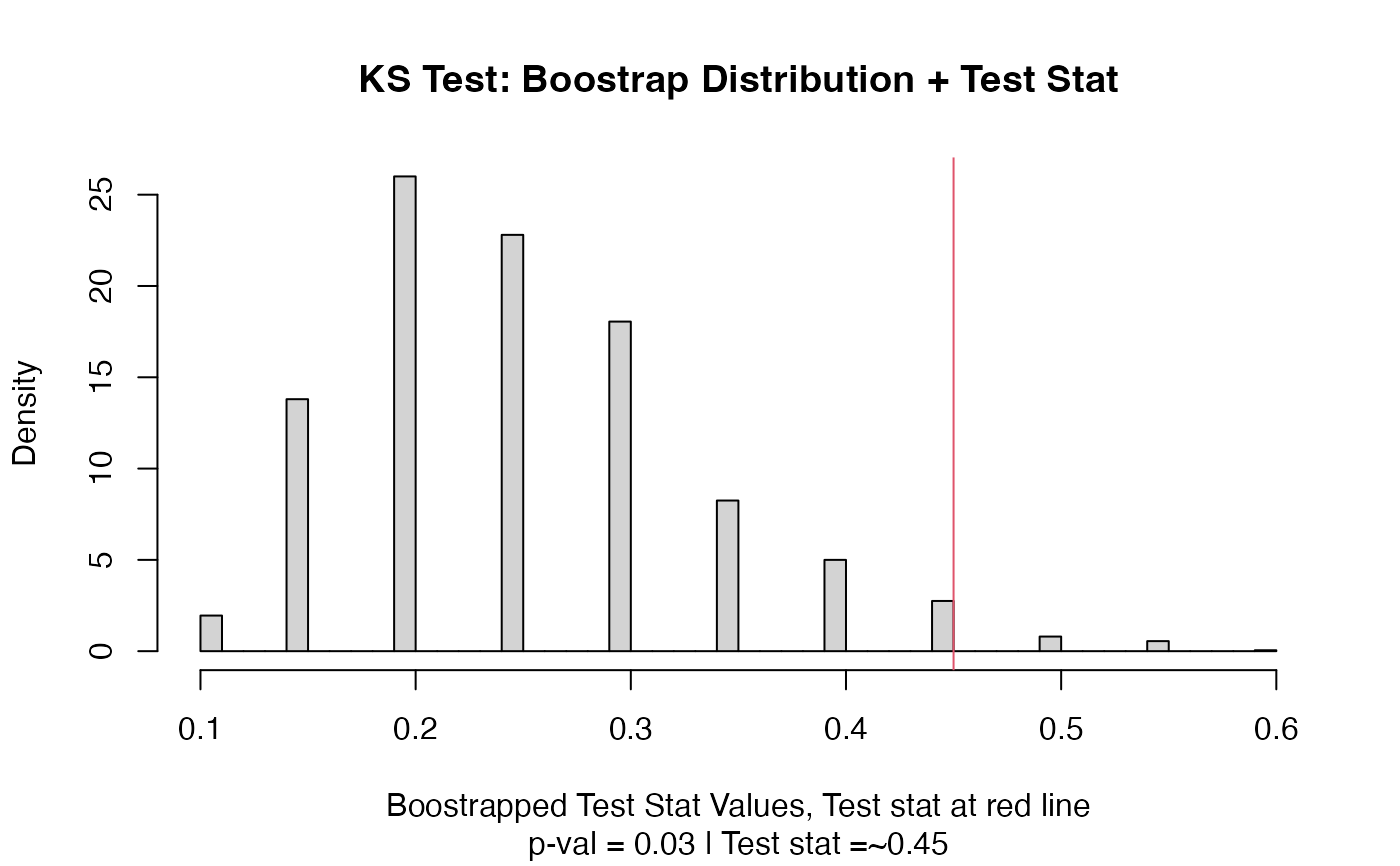
out = ks_test(vec1,vec2)
out
#> Test Stat   P-Value 
#>      0.45      0.03 
summary(out)
#> KS Test 
#> =========================
#> Test Statistic: 0.45 
#>        P-Value: 0.03 *
#> - - - - - - - - - - - - -
#>      n1      n2 n.boots 
#>      20      20    2000 
#> =========================
#> Test stat rejection threshold for alpha = 0.05 is: 0.4 
#> Null rejected: samples are from different distributions
plot(out)


# Example using ordered factors
vec1 = factor(LETTERS[1:5],levels = LETTERS,ordered = TRUE)
vec2 = factor(LETTERS[c(1,2,2,2,4)],levels = LETTERS, ordered=TRUE)
ks_test(vec1,vec2)
#> Test Stat   P-Value 
#>     0.400     0.716