Kuiper Test

A two-sample test based on the Kuiper test statistic (kuiper_stat).

Usage

kuiper_test(
  a,
  b,
  nboots = 2000,
  p = default.p,
  keep.boots = T,
  keep.samples = F
)

kuiper_stat(a, b, power = def_power)

Arguments

a

a vector of numbers (or factors -- see details)

b

a vector of numbers

nboots

Number of bootstrap iterations

p

power to raise test stat to

keep.boots

Should the bootstrap values be saved in the output?

keep.samples

Should the samples be saved in the output?

power

power to raise test stat to

Value

Output is a length 2 Vector with test stat and p-value in that order. That vector has 3 attributes -- the sample sizes of each sample, and the number of bootstraps performed for the pvalue.

Details

The Kuiper test compares two ECDFs by looking at the maximum positive and negative difference between them. Formally -- if E is the ECDF of sample 1 and F is the ECDF of sample 2, then $$KUIPER = |max_x E(x)-F(x)|^p + |max_x F(x)-E(x)|^p$$. The test p-value is calculated by randomly resampling two samples of the same size using the combined sample.

In the example plot below, the Kuiper statistic is the sum of the heights of the vertical black lines.

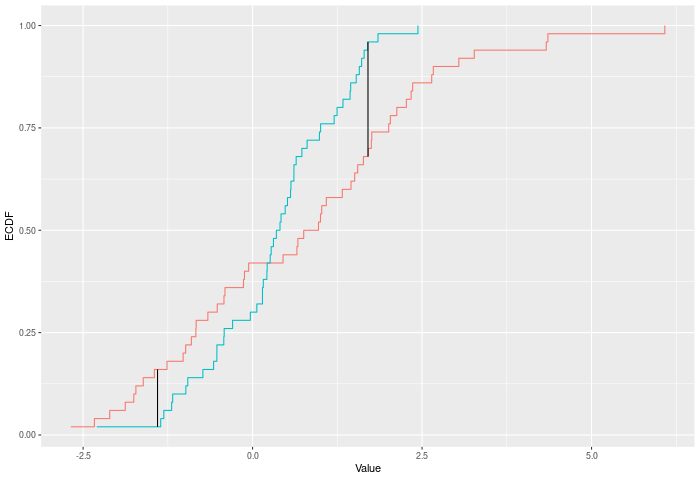
Inputs a and b can also be vectors of ordered (or unordered) factors, so long as both have the same levels and orderings. When possible, ordering factors will substantially increase power.

Functions

• kuiper_test(): Permutation based two sample Kuiper test

• kuiper_stat(): Permutation based two sample Kuiper test

See also

dts_test() for a more powerful test statistic. See ks_test() for the predecessor to this test statistic, and cvm_test() for its natural successor.

Examples

set.seed(314159)
vec1 = rnorm(20)
vec2 = rnorm(20,0.5)
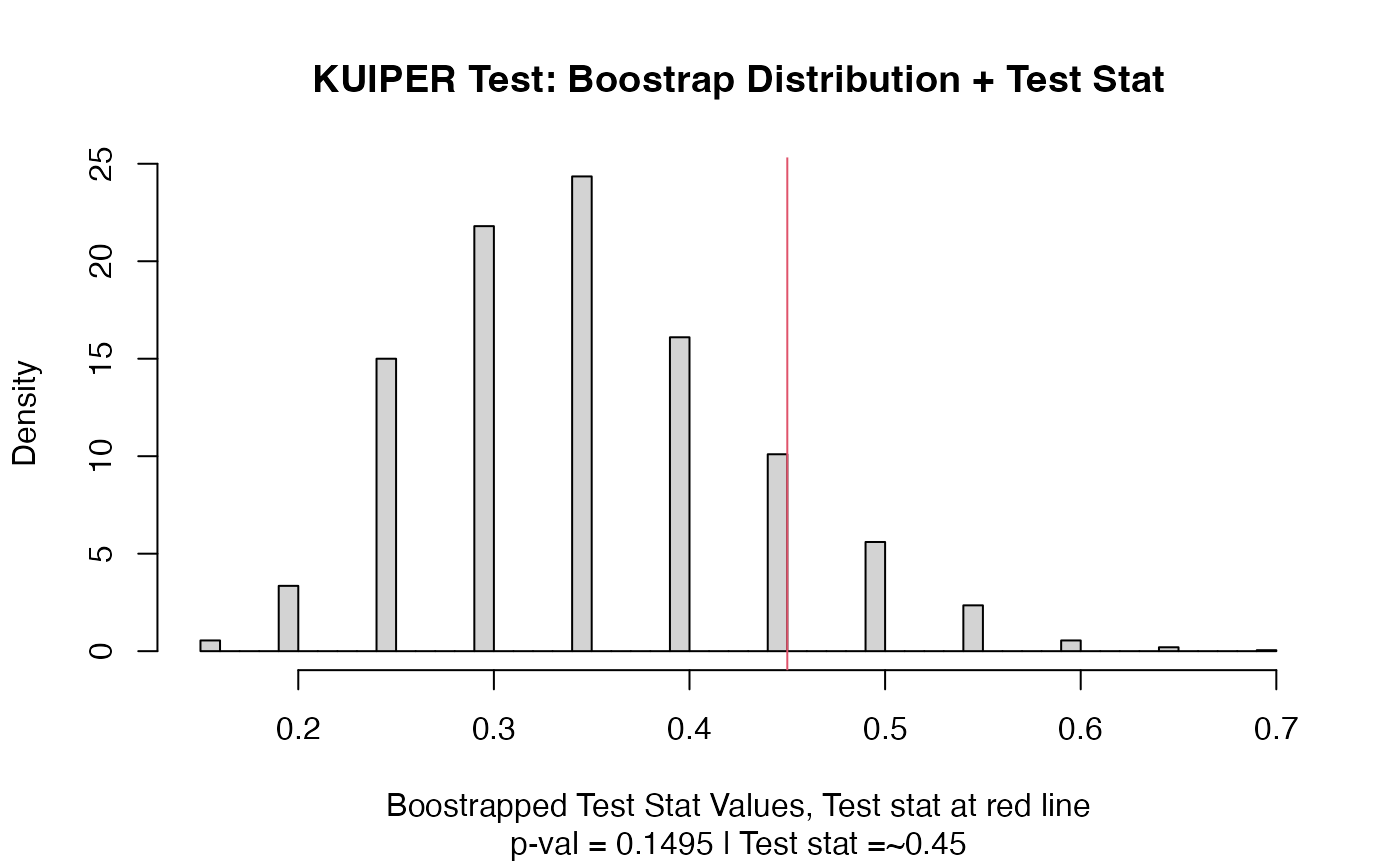
out = kuiper_test(vec1,vec2)
out
#> Test Stat   P-Value 
#>    0.4500    0.1495 
summary(out)
#> KUIPER Test 
#> =========================
#> Test Statistic: 0.45 
#>        P-Value: 0.1495 
#> - - - - - - - - - - - - -
#>      n1      n2 n.boots 
#>      20      20    2000 
#> =========================
#> Test stat rejection threshold for alpha = 0.05 is: 0.5 
#> Null not rejected: samples may be from same distribution
plot(out)



# Example using ordered factors
vec1 = factor(LETTERS[1:5],levels = LETTERS,ordered = TRUE)
vec2 = factor(LETTERS[c(1,2,2,2,4)],levels = LETTERS, ordered=TRUE)
kuiper_test(vec1,vec2)
#> Test Stat   P-Value 
#>     0.400     0.716